Satchel Grant

Emergent Symbol-like Number Variables in Artificial Neural Networks

Date Submitted: February, 2024
Journal/Venue: TMLR 2025

Satchel Grant, Noah D. Goodman, James L. McClelland

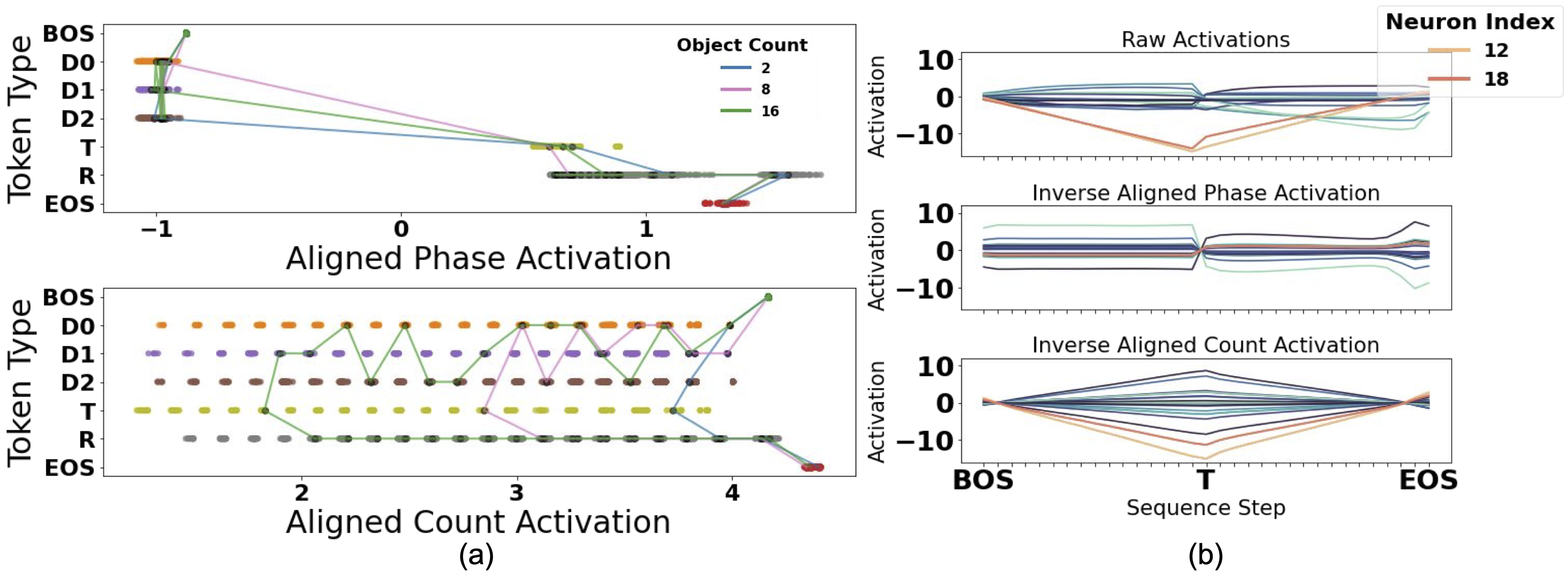
Abstract: What types of numeric representations emerge in neural systems, and what would a satisfying answer to this question look like? In this work, we interpret Neural Network (NN) solutions to sequence based number tasks through a variety of methods in an effort to understand how well we can interpret NNs through the lens of interpretable Symbolic Algorithms (SAs)––defined by precise, abstract, mutable variables used to perform computations. We use GRUs, LSTMs, and Transformers trained using Next Token Prediction (NTP) on numeric tasks where the solutions to the tasks vary in length and depend on numeric information only latent in the task structure. We show through multiple causal and theoretical methods that we can interpret NN's raw activity through the lens of simplified SAs when we frame the neural activity in terms of interpretable subspaces rather than individual neurons. Depending on the analysis, however, these interpretations can be graded, existing on a continuum, highlighting the philosophical quandry of what it means to "interpret" neural activity. We use this to motivate the introduction of Alignment Functions: invertible, learnable functions that add flexibility to the existing Distributed Alignment Search (DAS) framework. Through our specific analyses we show the importance of causal interventions for NN interpretability; we show that recurrent models develop graded, symbol-like number variables within their neural activity; we introduce Alignment Functions to frame NN activity in terms of general, invertible functions of interpretable variables; and we show that Transformers must use anti-Markovian solutions---solutions that avoid using cumulative, Markovian hidden states---in the absence of sufficient attention layers. We use our results to encourage NN interpretability at the level of neural subspaces through the lens of SAs.

I must admit that I'm proud of this work. It provides a satisfying answer to a question that has motivated a lot of my research: what does it mean to "understand the brain"? We provide the notion of Alignment Functions, which are invertible, learnable functions that establish an explicit relationship between neural activity and interpretable, understandable variables. I don't state this in the paper, but a nice definition of "understanding a concept" is the ability form that new concept in terms of a system of concepts that you already accept to be true. Alignment functions provide a way to learn such a relationship for neural activity.

Interpreting the retinal neural code for natural scenes: From computations to neurons

Date Published: Sept. 6, 2023
Journal/Venue: Neuron

Niru Maheswaranathan^*, Lane T McIntosh^*, Hidenori Tanaka^*, Satchel Grant^*, David B Kastner, Joshua B Melander, Aran Nayebi, Luke E Brezovec, Julia H Wang, Surya Ganguli, Stephen A Baccus

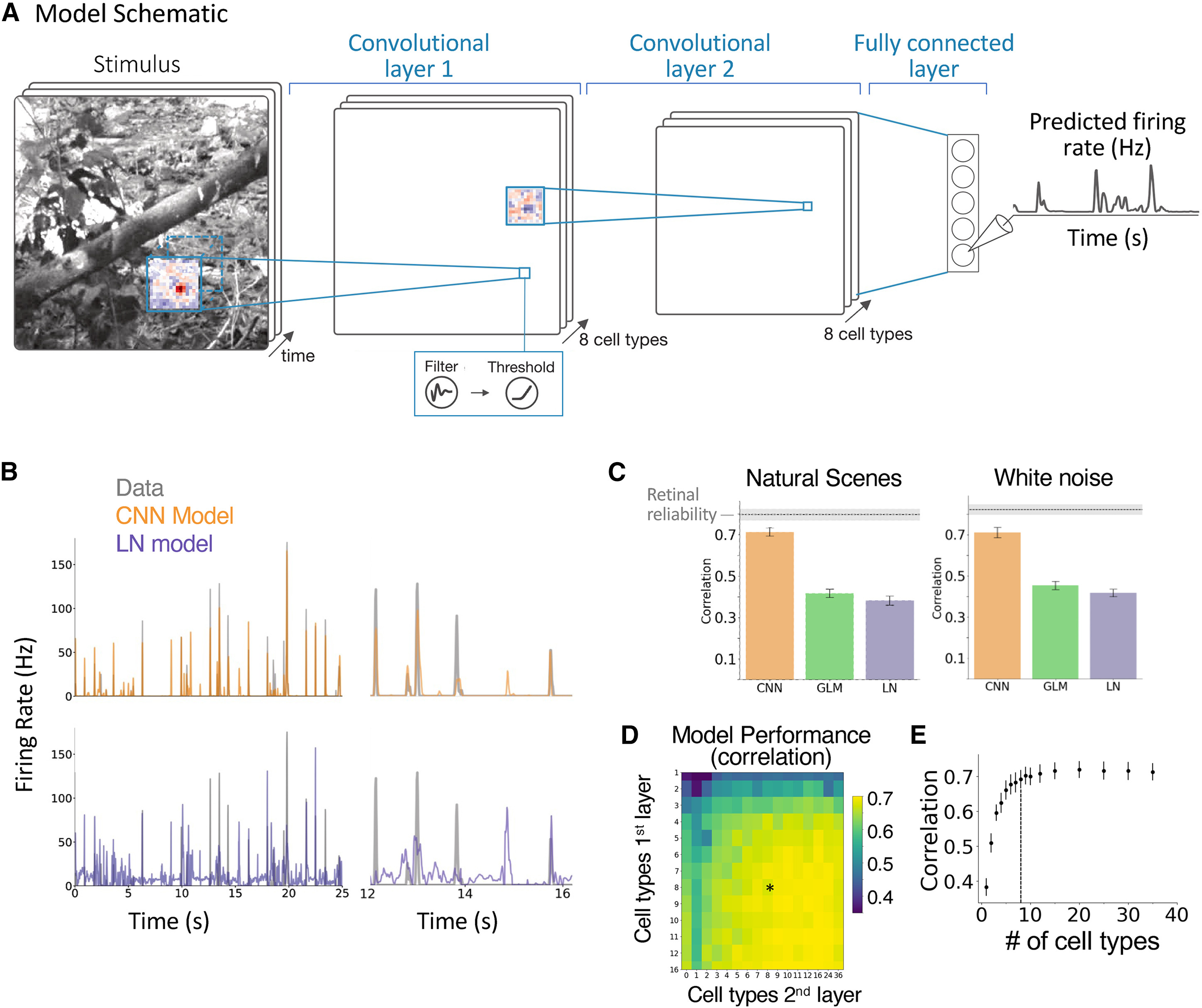
Abstract: Understanding the circuit mechanisms of the visual code for natural scenes is a central goal of sensory neuroscience. We show that a three-layer network model predicts retinal natural scene responses with an accuracy nearing experimental limits. The model’s internal structure is interpretable, as interneurons recorded separately and not modeled directly are highly correlated with model interneurons. Models fitted only to natural scenes reproduce a diverse set of phenomena related to motion encoding, adaptation, and predictive coding, establishing their ethological relevance to natural visual computation. A new approach decomposes the computations of model ganglion cells into the contributions of model interneurons, allowing automatic generation of new hypotheses for how interneurons with different spatiotemporal responses are combined to generate retinal computations, including predictive phenomena currently lacking an explanation. Our results demonstrate a unified and general approach to study the circuit mechanisms of ethological retinal computations under natural visual scenes.

This was a big collaboration over the course of many years. I love this work because it is a beautiful demonstration of how to establish an isomorphism between biological and artificial neural networks, and it shows how you can use that sort of model for interpreting the real biological neural code. I am a co-first author on this work for writing most of the project code, developing many architectural improvements, and developing much of the interneuron comparisons.

Model Alignment Search

Date Published: January 10, 2025
Journal/Venue: ICLR ReAlign Workshop 2025 (and under review at TMLR 2025)

Satchel Grant

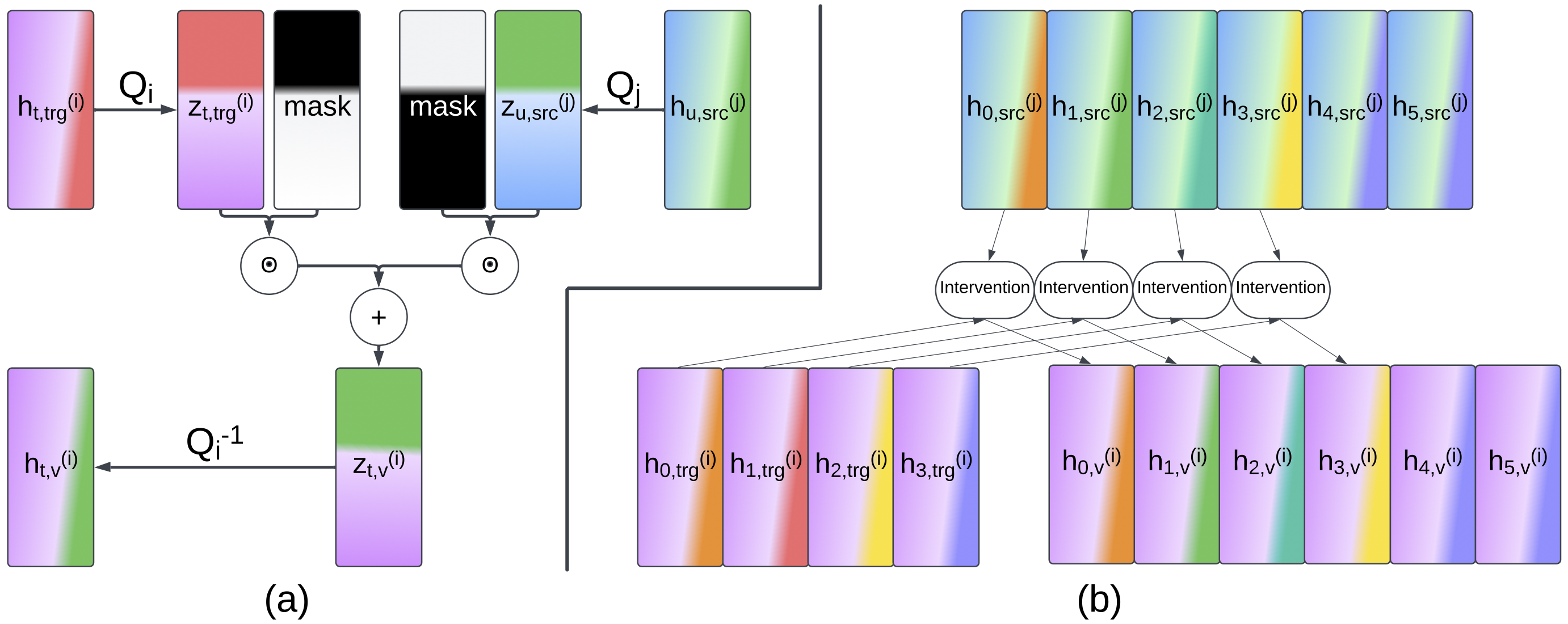
Abstract: When can we say that two neural systems are the same? What nuances do we miss when we fail to causally probe the representations of the systems? In this work, we introduce a method for connecting neural representational similarity to behavior through causal interventions. The method learns transformations that find an aligned subspace in which behavioral information can be interchanged between multiple distributed networks' representations. We first show that the method can be used to transfer the behavior from one frozen Neural Network (NN) to another in a manner similar to model stitching, and we show how the method can differ from correlative similarity measures like Representational Similarity Analysis. Next, we empirically and theoretically show how the method can be equivalent to model stitching when desired, or it can take a form that has a more restrictive focus to shared causal information; in both forms, it reduces the number of required matrices for a comparison of n models to be linear in n. We then present a case study on number-related tasks showing that the method can be used to examine specific subtypes of causal information, and we present another case study showing that the method can reveal toxicity in fine-tuned DeepSeek-r1-Qwen-1.5B models. Lastly, we show how to augment the loss with a counterfactual latent auxiliary objective to improve causal relevance when one of the two networks is causally inaccessible (as is often the case in comparisons with biological networks). We use our results to encourage the use of causal methods in neural similarity analyses and to suggest future explorations of network similarity methodology for model misalignment.

This is a followup to the Emergent Symbol-like Number Variables paper that allows us to causally compare representations between multiple neural systems and allows us to get closer to performing a DAS-like method on human brains. I feel the need to clarify that the sole-authorship was with the approval of my advisor, Jay McClelland. I offered for him to be a co-author, but he felt that he had not contributed enough to justify authorship (in part due to his stretched schedule). He is an extremely supportive advisor, and I am grateful for both the guidance and freedom that he has granted me. Similarly for Noah Goodman, who has been a great mentor and collaborator on the Emergent Symbol-like Number Variables paper, but who could not find the time to contribute to this work.

A mechanistically interpretable model of the retinal neural code for natural scenes with multiscale adaptive dynamics

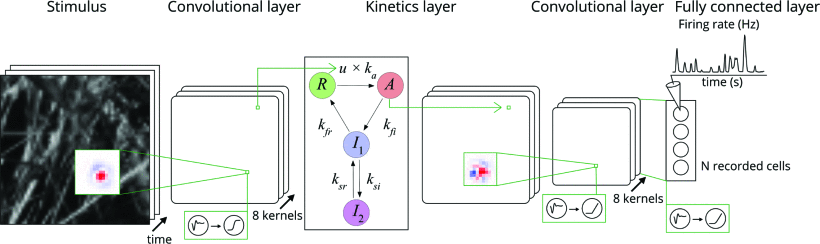Date Published: March 4, 2022
Journal/Venue: Asilomar

Xuehao Ding, Dongsoo Lee, Satchel Grant, Heike Stein, Lane McIntosh, Niru Maheswaranathan, Stephen Baccus

Abstract: The visual system processes stimuli over a wide range of spatiotemporal scales, with individual neurons receiving input from tens of thousands of neurons whose dynamics range from milliseconds to tens of seconds. This poses a challenge to create models that both accurately capture visual computations and are mechanistically interpretable. Here we present a model of salamander retinal ganglion cell spiking responses recorded with a multielectrode array that captures natural scene responses and slow adaptive dynamics. The model consists of a three-layer convolutional neural network (CNN) modified to include local recurrent synaptic dynamics taken from a linear-nonlinear-kinetic (LNK) model. We presented alternating natural scenes and uniform field white noise stimuli designed to engage slow contrast adaptation. To overcome difficulties fitting slow and fast dynamics together, we first optimized all fast spatiotemporal parameters, then separately optimized recurrent slow synaptic parameters. The resulting full model reproduces a wide range of retinal computations and is mechanistically interpretable, having internal units that correspond to retinal interneurons with biophysically modeled synapses. This model allows us to study the contribution of model units to any retinal computation, and examine how long-term adaptation changes the retinal neural code for natural scenes through selective adaptation of retinal pathways.

This project was a good extension of the CNN retinal model that I listed earlier. In this work, we managed to give the CNN model recurrence and used previous kinetics constants to get the model to exhibit slow adaptation (something that was lacking from the previous work).

Control and Predictivity in Neural Interpretability

Date Accepted: Sept 24, 2022
Journal/Venue: MechInterp Workshop NeurIPS 2025

Satchel Grant, Alexa Tartaglini

Abstract: For the goals of mechanistic interpretability, correlational methods are typically easy to scale and use, and can provide strong predictivity of Neural Network (NN) representations. However, they can lack causal fidelity which can limit their relevance to NN computation and behavior. Alternatively, causal approaches can offer strong behavioral control via targeted interventions, making them superior for understanding computational cause and effect. However, what if causal methods use out-of-distribution representations to produce their effects? Does this raise concerns about the faithfulness of the claims that can be made about the NN's native computations? In this work, we explore this possibility of this representational divergence. We ask to what degree do causally intervened representations diverge from the native distribution, and in what situations is this divergence acceptable? Using Distributed Alignment Search (DAS) as a case study, we first demonstrate the existence of causally intervened representational divergence in interventions that provide strong behavioral control, and we show that stronger behavioral control can correlate with more divergent intervened representations. We then provide a theoretical discussion showing sufficient ways for this divergence to occur in both innocuous and potentially pernicious ways. We then provide a theoretical demonstration that causal interventions typically assume principles of additivity, calling into question the use of nonlinear methods for causal manipulations. Lastly, for cases in which representational divergence is undesirable, we demonstrate how to incorporate a counterfactual latent loss to constrain intervened representations to remain closer to the native distribution. Together, we use our results to suggest that although causal methods are superior for most interpretability goals, a complete account of NN representations balances computational control with neural predictivity, with the optimal weighting depending on the goals of the research.

This particular writeup was accepted to the mech interp workshop at NeurIPS 2025. This is onlgoing work, however, and it will become an ICLR 2026 submission with expanded focus on causal interventions in general.

Discovering Functionally Sufficient Projections using Functional Component Analysis

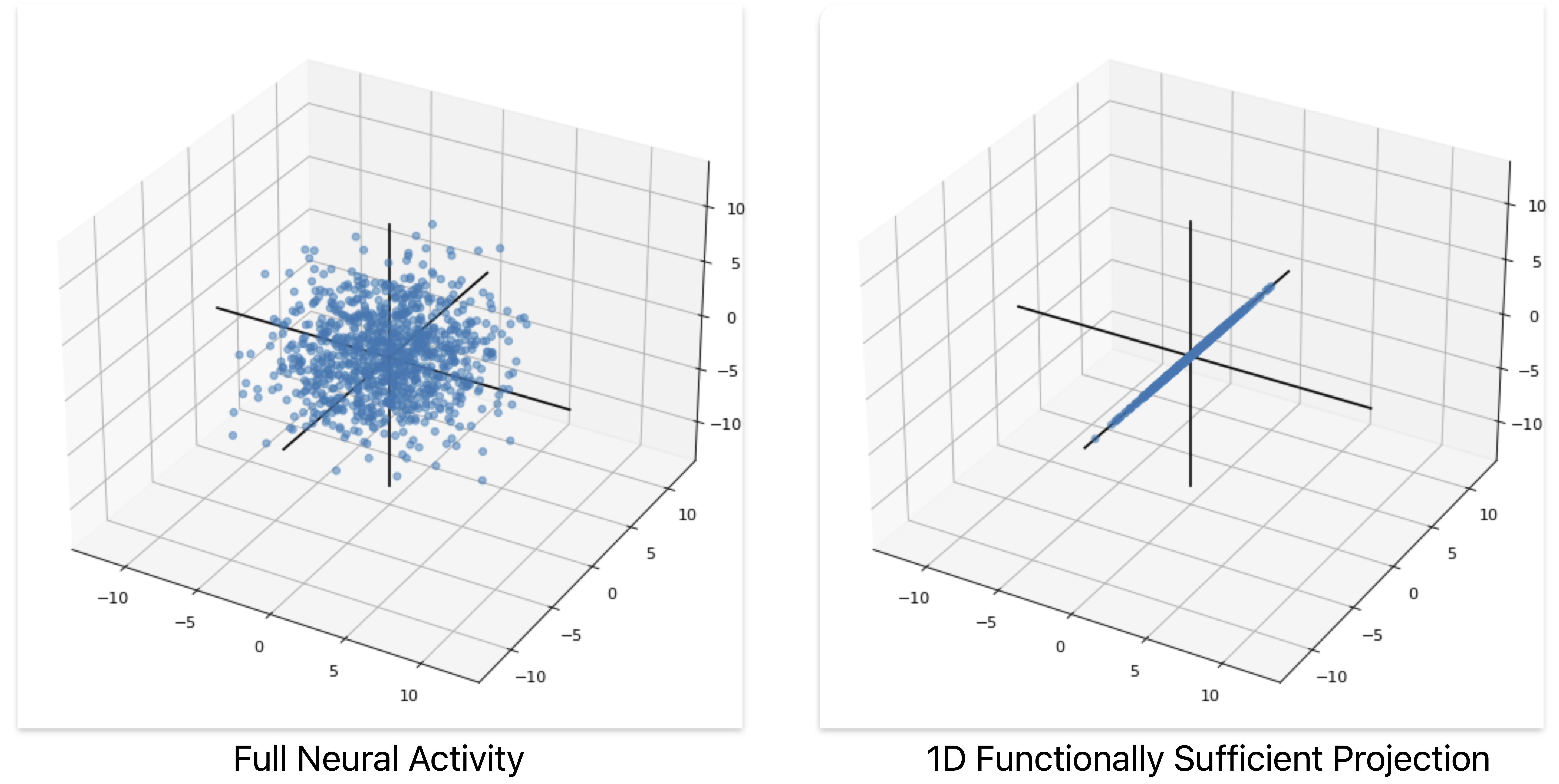Date Accepted: Sept 24, 2022
Journal/Venue: CogInterp NeurIPS Workshop 2025

Satchel Grant

Abstract: Many neural interpretability methods attempt to decompose Neural Network (NN) activity into vector directions or features along which variability serves to represent some interpretable aspect of how the NN performs its computations. In correlative analyses, these features can be used to classify what inputs and outputs correlate with changes in the feature; in casual analyses, these features can be used to causally influence computation and behavior. In both cases, it is easy to view these features as satisfying as ways to interpret NN activity. What if each feature, however, is an incomplete part of the story? For any given feature, is it necessary for the NN's computations, or is it only sufficient? In this work, we present a method for isolating Functionally Sufficient Projections (FSPs) in NN latent vectors, and we use a synthetic case study on MultiLayer Perceptrons (MLPs) to find that multiple, mutually orthogonal FSPs can produce the same behavior. We use the results of this work as a cautionary tale about claims of neural necessity.

Direct Manifold Capacity Optimization

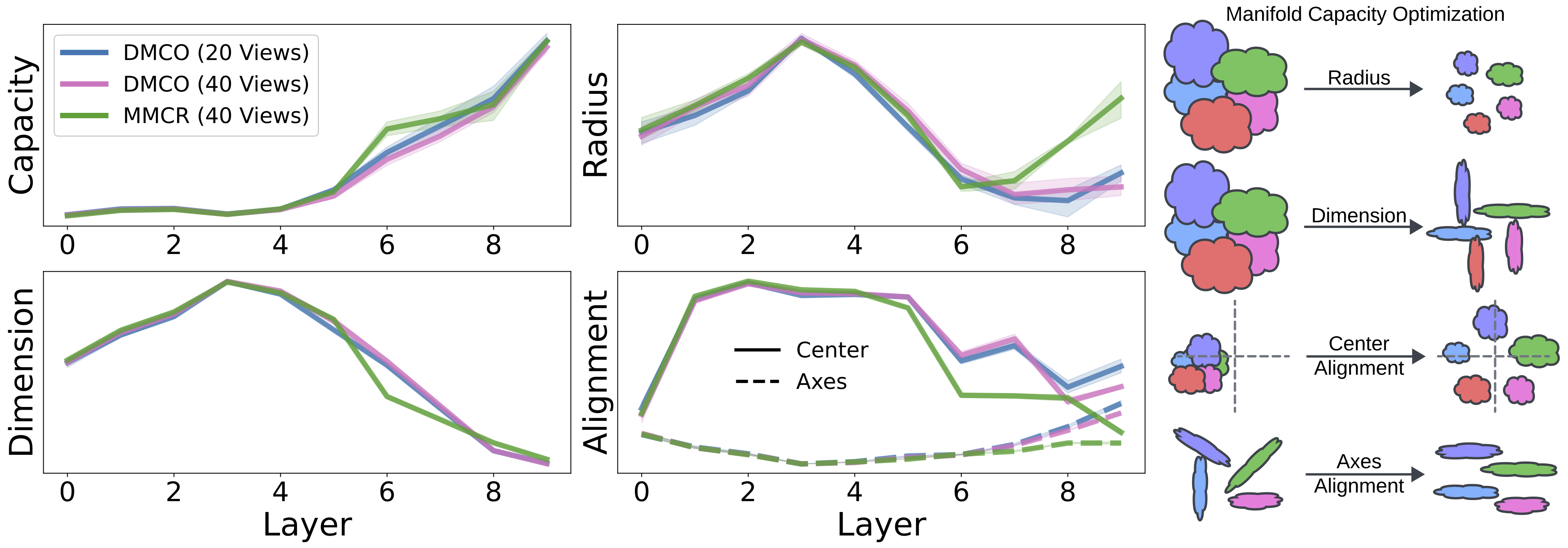Date: October 9, 2024

Satchel Grant, Chi-Ning Chou, Thomas Edward Yerxa, SueYeon Chung

Abstract: Manifold capacity is a tool for interpreting artificial and biological neural representations. Although the technique has shown utility in many analyses, an open question remains about whether the theory can also be used as a training objective for useful/robust neural representations. Previous work has made progress towards this goal in self-supervised learning settings by making assumptions about the shape of the manifolds. In this work, we use differentiable quadratic programming to maximize manifold capacity directly, without using simplifying assumptions. We show that our technique can match the overall performance of the pre-existing baselines with the ability to tune a hyperparameter to minimize the cumulative gradient steps or the total training samples. Our results show promise for exploring domains less suited to pre-existing simplifying assumptions, and our results add to the mounting evidence of manifold capacity as a powerful tool for characterizing neural representations.

This is ongoing work that will soon be submitted to a workshop.

Bidirectional Influences of Grounded Quantification and Language in Acquiring Numerical Cognitive Abilities

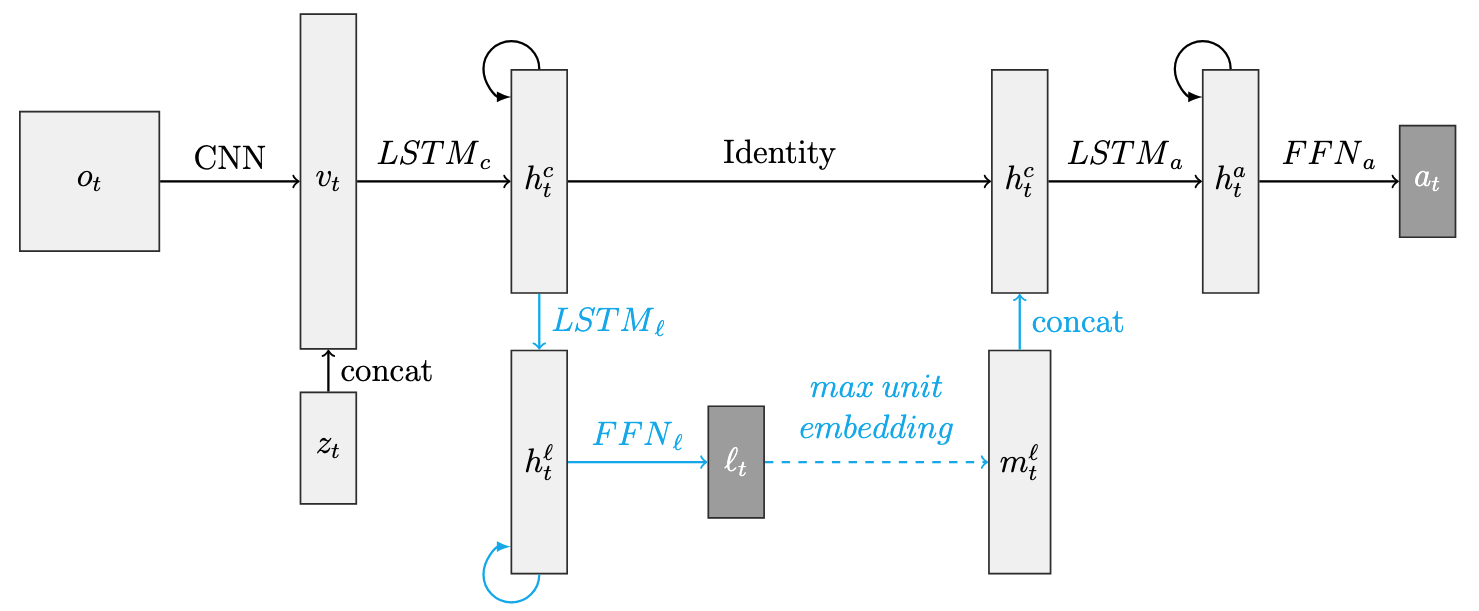Date Released: Dec 6, 2023

Satchel Grant, James L. McClelland

Abstract: We explore the role of language in cognition within the domain of number, revisiting a debate on the role of exact count words in numeric matching tasks. To address these issues, we introduce a virtual environment to simulate exact equivalence tasks like those used to study the numerical abilities of members of the Pirah˜a tribe, who lack exact number words, in previous works. We use recurrent neural networks to model visuospatially grounded counting behavior with and without the influence of exact number words. We find that it is possible for networks to learn to perform exact numeric matching tasks correctly up to non-trivial quantities with and without the use of exact number words. Importantly, however, networks with limited counting experience with and without language capture the approximate behavior exhibited by adult members of the Pirah˜a and young children learning to count in cultures with number words. Our networks also exhibit aspects of human numerical cognition purely through learning to solve the tasks: a flat coefficient of variation and a compressed mental number representation. We explore the causal influences of language and actions, showing that number words decrease the amount of experience needed to learn the numeric matching tasks, and learning the task actions reduces experience needed to learn number words. We use these results as a proof of principle for expanding our understanding of number cognition, and we suggest refinement to our collective understanding of the interactions between language and thought.

This is ongoing work that will soon be submitted to Cognition.

Leveraging Large Language Models for Context Compression

Date Released: May 31, 2023

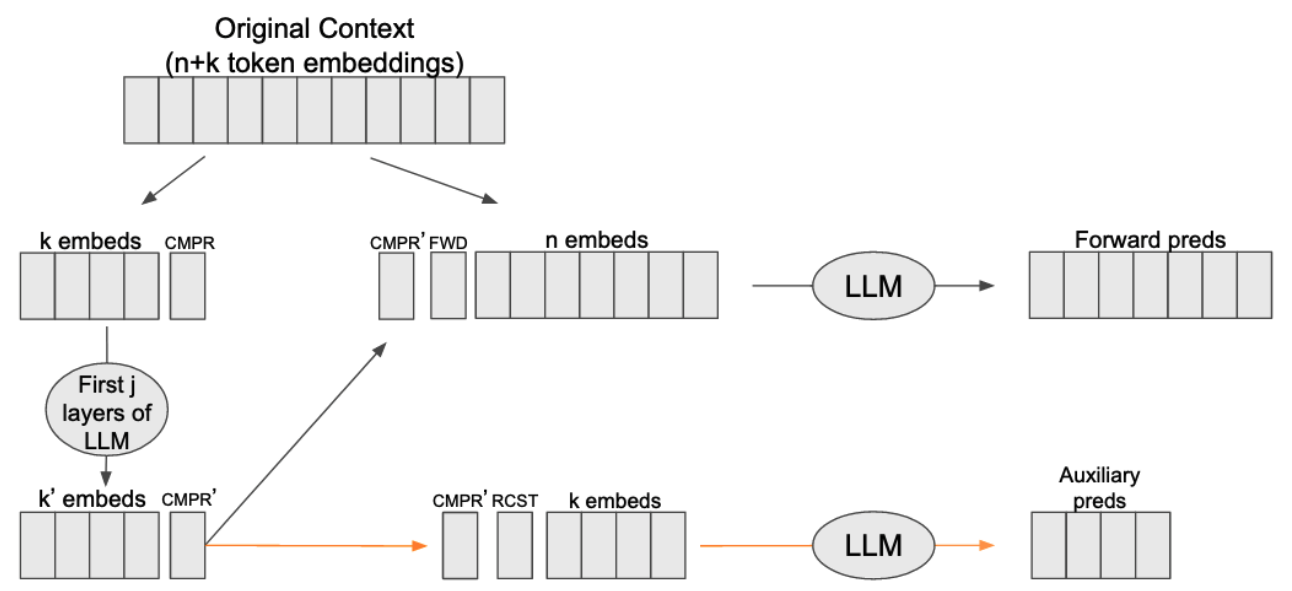
Abstract: Large Language Models (LLMs) have demonstrated remarkable performance on a wide range of language modeling tasks. LLMs have also demonstrated an ability to learn new tasks from clever prompt sequences, without the need for gradient updates. The length of an LLM's context window, however, has quadratic computational complexity, making large context windows prohibitively expensive. Furthermore, a problem with LLMs as models of cognition is their perfect memory for tokens within their context window, and their non-existant memory for things outside of their context window in the absence of weight updates. To address the challenges of large context windows, we introduce a technique that uses pretrained LLMs to create compressed, representations of sub-sequences within the context. We introduce a new token type that can be trained to compress a history of tokens at inference without additional gradient updates after training. These tokens serve to increase the context size while taking a step toward aligning LLMs with human stimulus abstraction. We use this technique to augment the open source Bloom models, and we show that the compressed representations can recover ~80\% of the performance of the LLMs using the full context.

I never submitted this to any conferences because it ended up being very similar to Jesse Mu's work, Learning to Compress Prompts with Gist Tokens. Then Alexis Chevalier et. al. published Adapting Language Models to Compress Contexts that does the exact same idea. Chevalier et. al. managed to scale things up very nicely, and had seemingly good results.

Spontaneous Decomposition from Grouped Network Pathways

Date Submitted: Dec, 2022 (hosted online Jul 1, 2022)

Abstract: There have been many recent breakthroughs in self- supervised learning (SSL), i.e. unsupervised techniques used to obtain general purpose image features for down- stream tasks. However, these methods often require large amounts of computational resources, and much is still unknown about how architectural choices affect the quality of self-supervised learned representations. There is still a lack of understanding of why compositional features spontaneously arise in previous self-supervised publications. In this work, we propose a class of models that is reminiscent of an ensemble. We show how this class of models can greatly reduce the number of parameters needed for learning robust representations in a self-supervised setting. Additionally, we show that sparsely connected network pathways spontaneously create decomposed representations.

In this work, we imposed network pathway grouping on a simple CNN architecture and found that different isolated subpathways would spontaneously learn distinct features of the training data. We also showed that this grouped pathway architecture had performance benefits over vanilla variants when holding parameter counts constant. We also made a poster here. I think this work was great, but we struggled with our message and audience. It was a project for Stanford's Computer Vision course so we attempted to frame the project as an architectural contribution, validating the representations on a performance benchmark (CIFAR10 image classification). I think the project is more interesting, however, for its qualtitative findings about learned representations. I still think this work has promise, but I'm not familiar with the greater literature. And since we completed this project, I think there has been some good theory work that could potentially explain our findings in terms of a Neural Race Reduction.

Improving Chain of Thought with Chain of Shortcuts

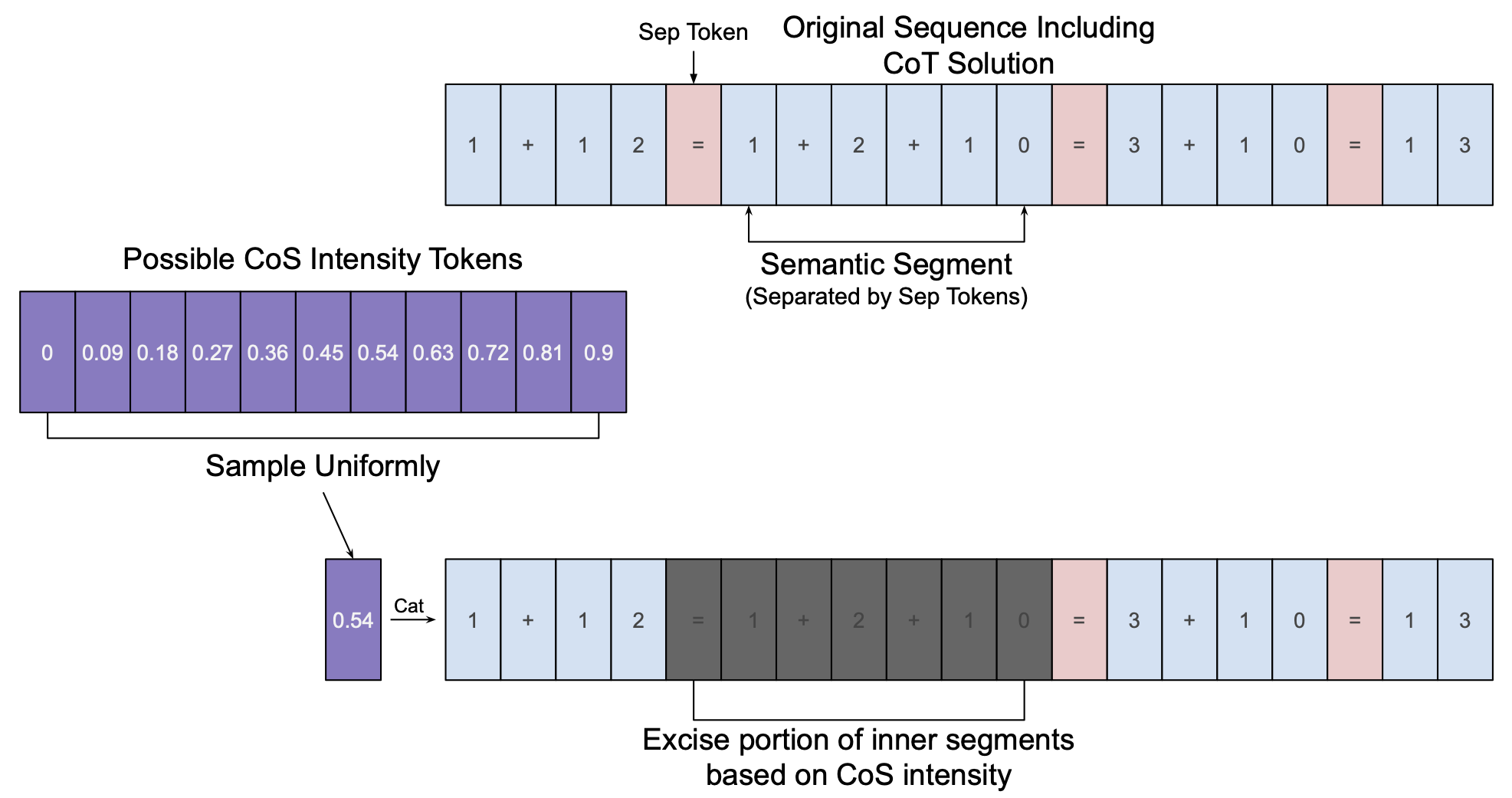Date Released: Dec 6, 2023

Abstract: Large Language Models (LLMs) have demonstrated remarkable language modeling and sequence modeling capabilities with capabilities like In-Context Learning (ICL) and Chain of Thought (CoT) reasoning, akin to human working memory and reasoning. Drawing inspiration from dual process theory in human cognition, we propose a novel training technique called Chain of Shortcuts (CoS) that bridges the gap between LLMs’ System 1 (automatic) and System 2 (deliberate) modes. CoS enables LLMs to compress reasoning trajectories, encouraging associations between earlier and later steps in problem-solving, resulting in shorter, more flexible solutions. We demonstrate that CoS-trained language models maintain or outperform baseline models while generating distilled problem solutions, enhancing stability during training, and excelling in high-temperature environments. CoS’s effectiveness increases with the number of transformer layers until saturation. Our work not only contributes to mathematical transformers but also offers insights into human dual process theory, paving the way for more efficient and robust AI systems.

Overall, this project's direction no longer seems promising as a longterm focus 😢 Another paper called GPT Can Solve Mathematical Problems Without a Calculator came out in September that essentially does what we were moving towards in terms of a Computer Science contribution. And the cognitive focus of this work is probably too abstract to be much of a contribution. This writeup was intended to be a NeurIPS workshop submission, but due to the reasons mentioned above, combined with a misinterpretation of the workshop deadline (12AM vs 12PM 😅), it was never submitted (and probably never will be).